a. Tên luận văn: Lý thuyết đa thế vị trên đa tạp Kähler
b.Họ và tên cá nhân thực hiện luận văn: Võ Quốc Hùng
c. Tên đơn vị công tác: Trường THPT Bình An
e. Kết quả thực hiện (tóm tắt)
Năm 1978 S.T. Yau giải quyết trọn vẹn giả thuyết Calabi (1956) về sự tồn tại của các metric Kähler với độ cong Ricci cho trước. Công trình của Yau đã mở rộng cánh cửa cho những ứng dụng của phương trình đạo hàm riêng vào lĩnh vực hình học vi phân hiện đại. Rất nhiều nhà toán học sau đó đã nghiện cứu bài toán Calabi-Yau trên các đa tạp không trơn. Việc đó đòi hỏi một nghiên cứu mới về phương trình MongeAmpère suy biến, nghĩa là các dữ kiện không phải là các hàm trơn nữa. Điều đó tạo động lực cho sự ra đời của lý thuyết đa thế vị trên đa tạp Kähler compact, lấy ý tưởng từ lý thuyết đa thế vị địa phương (trên n) được phát triển bởi E. Bedford và B.A. Taylor [1], [2]. Phần cốt lõi trong lý thuyết đa thế vị trên đa tạp là lý thuyết dung lượng và sự hội tụ của toán tử Monge-Ampère cũng như lớp các hàm kiểu Cegrell. Những đóng góp nổi bật nhất trong lĩnh vực này (nếu chỉ liệt kê vài người) thuộc về Kolodziej, Cegrell, Guedi-Zeriahi [12].
Cũng từ các nghiên cứu nền tảng của Bedford và Taylor, một vài tác giả đã nghiên cứu “lý thuyết đa thế vị” trên n (hoặc của đa tạp Stein). Lý thuyết này dùng để nghiên cứu các hàm đa điều hòa dưới (psh) và có thể xem như một sự tổng quát hóa phi tuyết tính của lý thuyết thế vị cổ điển (trên mặt phẳng phức), trong đó các hàm điều hòa dưới và toán tử Laplace .bmp) được thay thế bởi các hàm psh và toán tử MongeAmpère phức (dd c)n . Ở đây d, dc là ký hiệu của các toán tử vi phân thực
được thay thế bởi các hàm psh và toán tử MongeAmpère phức (dd c)n . Ở đây d, dc là ký hiệu của các toán tử vi phân thực 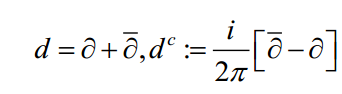 từ đó
từ đó  ; tiêu chuẩn được chọn để độ đo dương
; tiêu chuẩn được chọn để độ đo dương  có giá trị 1 trên Cn.
có giá trị 1 trên Cn.
Mục đích của luận văn là trình bày một lý thuyết thế vị toàn cục trên đa tạp Kähler compact. Từ nguyên lý cực đại ta biết rằng không có hàm đa điều hòa dưới nào (trừ hàm hằng) trên một đa tạp phức compact X . Tuy nhiên, có nhiều dòng dương đóng có song bậc (1,1) trên đó. Cho  là một dòng trơn đóng thực có song bậc (1,1) trên X , ta xét các dòng đóng dương
là một dòng trơn đóng thực có song bậc (1,1) trên X , ta xét các dòng đóng dương  có song bậc (1,1) trên X đối đồng điều với
có song bậc (1,1) trên X đối đồng điều với .bmp) . Khi X là Kähler , theo “bổ đề ddc ” thì
. Khi X là Kähler , theo “bổ đề ddc ” thì  có thể được viết thành
có thể được viết thành  =+ ddc , với
=+ ddc , với  là một hàm khả tích đối với mọi dạng thể tích trơn trên X . Một hàm
là một hàm khả tích đối với mọi dạng thể tích trơn trên X . Một hàm  như vậy được gọi là
như vậy được gọi là  - đa điều hòa dưới (
- đa điều hòa dưới ( -psh). Về mặt địa phương thì một hàm
-psh). Về mặt địa phương thì một hàm  -psh là tổng của một hàm psh và một hàm trơn. Ta ký hiệu tập hợp các hàm
-psh là tổng của một hàm psh và một hàm trơn. Ta ký hiệu tập hợp các hàm  -psh là PSH (X ,
-psh là PSH (X , ). Các hàm như vậy được giới thiệu bởi Demailly, và được gọi là các hàm tựa đa điều hòa dưới (qpsh).
). Các hàm như vậy được giới thiệu bởi Demailly, và được gọi là các hàm tựa đa điều hòa dưới (qpsh).
Trong phần kiến thức chuẩn bị, tác giả đã trình bày một số tính chất của hàm đa điều hòa dưới: Độ đo Radon (độ đo Borel, các phiếm hàm tuyến tính dương trên C0(X), Tôpô yếu trên không gian các độ đo; hàm điều hòa (định nghĩa và tính chất cơ bản, công thức Poisson và bất đẳng thức Harnack, nguyên lý cực đại, bài toán Dirichlet trên đĩa); hàm điều hòa dưới (định nghĩa và tính chất cơ bản, nguyên lý cực đại, công thức biểu diễn Riesz, công thức Poisson-Jensen); hàm đa điều hòa dưới (tính chất cơ bản, bất đẳng thức giá trị trung bình dưới, xấp xỉ trơn các hàm đa chiều dưới, Topo trên PSH ( ), tính bất biến, Bổ đề Hartogs và tính chất Montel, So sánh các tôpô trên PSH(
), tính bất biến, Bổ đề Hartogs và tính chất Montel, So sánh các tôpô trên PSH( ), số Lelong; dạng vi phân với hệ số là các phân bố; dòng đóng; song bậc; dạng dương; dòng dương; ví dụ về dòng dương.
), số Lelong; dạng vi phân với hệ số là các phân bố; dòng đóng; song bậc; dạng dương; dòng dương; ví dụ về dòng dương.
Về nội dung Đa tạp Kähler compact, tác giả trình bày một số khái niệm và kết quả cơ bản về đa tạp Kähler. Để định nghĩa đa tạp Kähler, ta có thể xuất phát từ một đa tạp phức: Một đa tạp phức được gọi là Kähler nếu trên đó tồn tại một (1,1) -dạng vi phân trơn, đóng, và xác định dương. Một dạng vi phân như thế sẽ được gọi là dạng Kähler. Trong rất nhiều trường hợp, ta có một đa tạp thực 2n chiều và ta muốn biết liệu có thể trang bị một cấu trúc Kähler trên đa tạp đó hay không.
Một metric Hermit h trên đa tạp hầu phức (M,J) là một metric Riemann trên M tương thích với cấu trúc hầu phức J, nghĩa là 
Từ metric Hermit h ta định nghĩa một 2 -dạng cơ bản  bởi
bởi  (X,Y) := h(JX,Y). Metric h được gọi là Kähler nếu d 0 và tensor J là khả tích.
(X,Y) := h(JX,Y). Metric h được gọi là Kähler nếu d 0 và tensor J là khả tích.
Ta mở rộng metric Hermit h C- tuyến tính lên TMC và vẫn ký hiệu là h. Ta có: .bmp)
Giả sử h là một (0,2) tensor đối xứng trên TMC thỏa mãn ba điều kiện trên. Khi đó hạn chế của h lên TM là một metric Hermit.
Trên mọi đa tạp hầu phức (M,J) đều tồn tại một metric Hermit. Thật vậy, ta chỉ cần chọn một metric Riemann g rồi đặt h(X Y)=g(X,Y)+ g(JX,JY).
Trong phần lý thuyết đa thế vị trên đa tạp Kähler compact, chúng ta xét X là một đa tạp Kähler compact liên thông số chiều n. Khái niệm đa điều hòa dưới của một hàm u: U →R là bất biến qua một tự đồng cấu chỉnh hình của Cn. Do đó ta có thể định nghĩa thế nào là một hàm đa điều hòa dưới trên một đa tạp phức.
Cụ thể là: một hàm U .bmp) L1(X) là đa điều hòa dưới trên X nếu u nửa liên tục trên và trên mỗi lân cận địa phương (U,
L1(X) là đa điều hòa dưới trên X nếu u nửa liên tục trên và trên mỗi lân cận địa phương (U, .bmp) ) hàm u0
) hàm u0 .bmp) -1 là điều hòa dưới trên U. Ta kiểm tra được định nghĩa trên không phụ thuộc vào việc chọn tọa độ địa phương do các phép biến đổi tọa độ là chỉnh hình. Tuy nhiên theo nguyên lý cực đại thì trên một đa tạp phức compact mọi hàm đa điều hòa dưới đều là hàm hằng. Cho
-1 là điều hòa dưới trên U. Ta kiểm tra được định nghĩa trên không phụ thuộc vào việc chọn tọa độ địa phương do các phép biến đổi tọa độ là chỉnh hình. Tuy nhiên theo nguyên lý cực đại thì trên một đa tạp phức compact mọi hàm đa điều hòa dưới đều là hàm hằng. Cho  là một dòng thực đóng có song bậc (1,1) trên X. Thay vì nghiên cứu các hàm đa điều hòa dưới trên X ta sẽ nghiên cứu một lớp hàm rộng hơn nhiều: hàm
là một dòng thực đóng có song bậc (1,1) trên X. Thay vì nghiên cứu các hàm đa điều hòa dưới trên X ta sẽ nghiên cứu một lớp hàm rộng hơn nhiều: hàm  -đa điều hòa dưới.
-đa điều hòa dưới.
Trong luận văn, tác giả đã giới thiệu được những nội dung cơ bản của lý thuyết đa thế vị trên đa tạp Kähler là lý thuyết dung lượng và sự hội tụ của toán tử Monge-Ampère, trong đó các kiến thức chuẩn bị để tìm hiểu và giải quyết các vấn đề được trình bàykhá chi tiết đó là: Các tính chất cơ bản của hàm đa điều hòa dưới; Lý thuyết về Dòng dương; Các kiến thức cơ bản về đa tạp Kähler.
Lý thuyết dung lượng và sự hội tụ của toán tử Monge-Ampère cũng đã được trình bày khá chi tiết mà chủ yếu là các vấn đề như: Định nghĩa toán tử Monge-Ampère (theo lý thuyết địa phương của BedfordTaylor; Các tính chất cơ bản của dung lượng Monge-Ampère và công thức tính dung lượng ngoài; Sự hội tụ của toán tử Monge-Ampère theo dãy tăng, dãy giảm và dãy hội tụ theo dung lượng.
g. Năm tốt nghiệp: 2015
(Có thể tìm đọc toàn văn Báo cáo luận văn tại Trung tâm Thông tin và Thống kê khoa học và công nghệ).